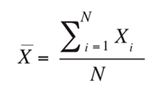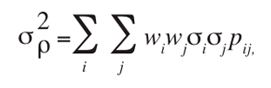Med skråblikk på samfunn og økonomi.
January 30, 2013 Leave a comment
Aksjemarkedet har hatt en høy samvariasjon med konsumtillits-indeksen, og dermed har sistnevnte vist seg å være en forholdsvis god økonomisk indikator.
Nå har utviklingen i aksjemarkedet dratt av gårde med en sterk vekst, mens konsumentene er langt mindre optimistiske til fremtiden. Har optimistene i aksjemarkedet tatt sats for tidlig, eller ser ikke konsumentene lyset i tunnellen?
January 30, 2013 Leave a comment
Finanskrisen har resultert i at store deler av den vestlige verden har havnet i en kraftig nedgangskonjunktur. Resultatet er høy arbeidsledighet og store nasjonale budsjettunderskudd gjennom kraftig reduksjon i skatteinntekter. Tradisjonelt er de virkmidler som står til rådighet enten finanspolitiske eller pengepolitiske. Klassiske finanspolitiske tiltak er å øke offentlige utgifter, f.eks. utbygging av offentlig infrastruktur, mens pengepolitiske tiltak skal bidra til økte investeringer gjennom lavere renter. Begge typer tiltak har som formål å bidra til økt økonomisk aktivitet, og derigjennom bidra til at en nedadgående økonomi snur og igjen begynner å ekspandere.
Fordi mange nasjoner har satt seg i en betydelig gjeldsposisjon, har de begrensede muligheter til å stimulere økonomien med finanspolitiske tiltak. De reduserte skatteinntektene og den manglende lånekapasiteten gjør det vanskelig nok å opprettholde det eksisterende utgiftsnivået, og nærmest umulig å øke det.
Nasjoner som har sin egen valuta har også muligheten til å stimulere økonomien med pengepolitiske tiltak. Pengetilførselen skjer ved at sentralbanken foretar store obligasjonskjøp i markedet. Dette gjør at prisen på disse papirene stiger, og rentene synker. For den samlede økonomien vil lavere renter gjøre det mindre attraktivt å spare, og billigere å låne. Effekten gir økte investeringer og konsum, og dermed vekstimpulser til økonomien.
I tillegg til den stimulerende effekten som lavere renter har på økonomien, så bidrar den til en mindre attraktiv valuta. Dette til glede for landets eksportører som får økte inntekter fra sitt internasjonale salg og derav styrket sin konkurranseevne. I realiteten er dette en god gammeldags devaluering, som ikke skjer over natten men over tid. Man skal kanskje ikke utelate at dette er en medvirkende årsak til at USA har valgt å kalle sine pengepolitiske tiltak for ‘Quantitative Easing’ (kvantitative lettelser). Det høres jo ganske uskyldig ut. Kina derimot har på ingen måte latt seg lure. Selv om de er tjent med et økonomisk sterkt USA, så kommer det tydelige signaler om at man ser på de amerikanske tiltakene som en form for snik-devaluering, og da blant annet på bekostning av fremvoksende økonomier. Kritiske røster i USA har derimot tidligere beskyldt Kina for å holde sin valuta kunstig lav, og derav hatt en “devaluerende effekt”.
Siste nasjon ut er Japan, som har hevet inflasjonsmålet sitt fra 1% til 2%. Et pengepolitisk tiltak som signaliserer til markedet at man vil være mindre tilbøyelig enn før til å øke rentene når man ser inflasjonstendenser i økonomien. Reduserte japanske renter har gitt en svekket japansk valuta, til glede for japansk eksportindustri.
Forhåpentligvis er det ikke en valutakrig vi ser tendenser til.
January 28, 2013 Leave a comment
Det er ikke alltid det er like lett å forstå alle ord og uttrykk som brukes av økonomene. Dette er begrepene fiscal cliff og debt ceiling forklart på en hverdagslig og billedlig måte.
January 26, 2013 Leave a comment
The Economist: Has Apple peaked?
Etter å ha klatret til posisjonen som verdens mest verdifulle børsnoterte selskap på slutten av 2012, så mistet Apple posisjonen igjen i forbindelse med fremleggelsen av Q4’12-tallene. En økende andel av markedet tror at toppen for selskapet nå er passert, som primært begrunnes med to forhold.
For det første er det usikkerhet til om Steve Jobs’ død vil redusere selskapets innovasjonsevne. I selskapets markedsverdi ligger en ganske stor forventning om at man vil lansere nye revolusjonerende produkter som man klarer å ta ut en superprofit av i markedet.
For det andre forventes superprofiten på dagens produkter å gradvis reduseres gjennom tøffere konkurranse (mean reversion).
Til nå har Apple hatt imponerende vekst og marginer. Samtidig har selskapets verdimultipler vært relativt normale, og indikert at selskapet har vært fair priset. Hvis derimot forventet vekst og marginer ikke kan opprettholdes, så vil både mulipler og verdi trekke inn.
January 25, 2013 Leave a comment
Kommentar av Rögnvaldur Hannesson (professor NHH) i E24 om realiteter rundt fornybar og ikke-fornybar energi. Bl.a. om hvorvidt fornybar energi, og da ikke bare sol- og vindkraft men også biobrensler, vil kunne erstatte fossile brensler. Påstanden er at de som har veddet på snarlig slutt på de fossile brenslers tidsalder har nok veddet på feil hest.
January 25, 2013 Leave a comment
Hvordan man lykkes i livet er avhengig av så mange ting. Vi liker å tro at hardt arbeid og talent er de vesentligste faktorene, sammen med den litt ubestemmelige faktoren flaks. Det siste er imidlertid litt vanskelig å forholde seg til, da det ligger helt utenfor vår kontroll. Talent ligger delvis også utenfor vår kontroll, da det er noe vi har med oss gjennom arv, men hvordan vi utnytter talentet ligger derimot klart innenfor vår kontroll. Det samme gjelder definitivt også faktoren hardt arbeid, som for de fleste av oss synes å ha størst betydning for hvordan livet vil forløpe. Heldigvis vil de fleste av oss si.
Det bør være liten uenighet om at man er tjent med at det organiserte samfunnet legger til rette for at man i størst mulig grad skal kunne få forløst hardt arbeid og talent. For individet vil innsatsen bli innkassert gjennom en høyere inntekt og et bedre liv. For landet som helhet, som er summen av individene, vil det gi en tilsvarende høyere nasjonalinntekt (BNP).
Hvordan de enkelte land har valgt å organiserer sitt samfunnet er imidlertid forskjellig, og en av disse forskjellene er hvilken grad av likhet mellom landets innbyggere man innretter seg på. Når både evne og vilje til å skape økonomiske verdier er ulikt fordelt i befolkningen, så vil likhetsinnretningen i samfunnet måtte involvere en omfordeling gjennom skatter. Jo mer likhet man ønsker, jo mer verdier må flyttes fra de som skaper mest, til de som skaper minst. Overføringer andre veien har vi ikke hatt siden de gamle føydalsamfunnene, og da skjedde overføringen med våpen i hånd. Forklaringene til hvorfor landene forholder seg forskjellig til dette med ulikheter mellom innbyggerne er mange. Faktorer som ofte trekkes frem fra land med stor ulikhet er synet på individet og rettferdighet, samt at verdioverføring i seg selv hevdes å ha en reduserende effekt på den samlede verdiskapingen. Jo mindre individet får beholde av den verdi som skapes, jo mindre er han villig til å nedlegge av nødvendig arbeid og talent for å skape verdien. Faktorer som trekkes frem fra land med stor likhet er synet på fellesskapet og rettferdighet (motsatt rettferdighetsargument som over), og at ulikhet begrenser evnen til å få utløst talent og hardt arbeid fra alle deler av samfunnet.
Den økonomiske forskningen synes nå å ha gitt ytterligere fakta til det siste spørsmålet.
Økonomen Alan Krueger (rådgiver for Obama og professor ved Princeton University) introduserte i 2012 en grafisk illustrasjon av temaet kalt ’The Great Gatsby Curve’. Navnet på kurven henviser til F. Scott Fitzgeralds roman The Great Gatsby der den fattige hovedpersonen Jay Gatsby (født Gatz), klatrer på den sosiale stigen i miljøet på den nordlige kysten av Long Island.
Diagrammet viser sammenhengen mellom innteksmessig ulikhet og økonomisk mobilitet mellom generasjoner for ulike land.
Den horisontale aksen i diagrammet er et mål for økonomisk ulikhet kalt Gini-koeffisienten. Denne måles på en skala fra 0 til 1, der 0 er perfekt likhet (alle mennesker har samme inntekt), og 1 er perfekt ulikhet (en person har all inntekt). Den vertikale aksen av diagrammet er et mål for økonomisk mobilitet på tvers av generasjoner. Dette måles ved ’Intergenerational earnings elastisity (IGE)’, som er definert som den prosentvise forskjellen i et barns inntekt ved en 1 prosent forskjell i foreldrenes inntekt. En IGE på 0,4 betyr at hvis en far tjente 20 prosent mer enn en annen over deres levetid, vil den første fars sønn i gjennomsnitt tjene 8 prosent mer enn den andre fars sønn, og en IGE på 0,6 betyr at den første fars sønn ville tjene 12 prosent mer i gjennomsnitt enn andre fars sønn. Det vil si jo høyere IGE er, jo lavere er den økonomiske mobiliteten mellom generasjoner.
Som vi ser er sammenhengen i diagrammet sterk, med enn høy korrelasjon (R2=0,76). Det grunnleggende budskapet i The Great Gatsby Curve er at land som har et høyere nivå av inntektsulikhet på et tidspunkt (Gini-koeffisienten på den horisontale aksen), vil også tendere til å ha en mindre økonomisk mobilitet mellom generasjoner (IGE-forhold på den vertikale aksen).
En utvidet forklaring av sammenhengen mellom inntektsulikhet og lav økonomisk mobilitet, er at foreldre med høy utdanning, og derav også høy inntekt, i større grad fokuserer og oppmuntrer sine barn til også å satse på utdanning for å sikre seg et liv med økonomisk sikkerhet.
Et nærliggende spørsmål for forskerne å forfølge videre er om land med inntektslikhet har et konkurransefortrinn i forhold til land med ulikhet. Finnes det et optimalt nivå for likhet/ulikhet hvor verdiskapingen i samfunnet som helhet er størst?
January 23, 2013 Leave a comment
Porteføljeavkastning
Den totale avkastningen for en portefølje som består av flere aktiva, beregnes som den vektede summen av avkastningen til samtlige aktiva:
Der wi er vekten av aktivum i (andelen i porteføljen). Ri er avkastningen på aktivum i. Eksempel: Anta at en portefølje inneholder tre aktiva som har gitt en avkastning på henholdsvis 9 prosent, 12 prosent og 18 prosent. De tre aktivaene har like stor vekt i porteføljen. Porteføljens avkastning beregnes da som: (1/3 x 9 prosent + 1/3 x 12 prosent + 1/3 x 18 prosent = 13 prosent).
Prisrisiko
Prisrisiko er aktivaprisens svingninger i forhold til sin middelverdi, aktivumets volatilitet. En aksjes volatilitet angir i hvilken grad aksjens kurs avviker fra sin middelverdi. Volatiliteten gjenspeiler både positive og negative svingninger, og har dermed ikke noe å gjøre med opp- eller nedgang, men er kun et mål på kursbevegelsenes størrelse. Store kursbevegelser er lik med stor risiko, mens et aktivum med en helt lineær prisutvikling har en volatilitet på null. Volatilitet måles som et aktivas standardavvik, og for å beregne standardavviket må man først regne ut middelverdien:
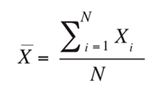
Der Xi er prisen på aktivum X ved observasjon i og N er antallet observasjoner. Standardavviket er roten av den vektede summen av de gjenstående avvikene fra middelverdien.
I og med at avvikene er kvadrert, kan standardavviket ikke bli negativt.
Porteføljerisiko
Som vist over så er en porteføljes avkastning den vektede summen av hver enkelt instruments avkastning. Dette gjelder imidlertid ikke for porteføljens totale risiko. I så fall skulle en portefølje med to verdipapirer med like høy volatilitet ha samme volatilitet som de enkelte? Dette gjelder kun i tilfeller da instrumentene har en perfekt korrelasjon (samvariasjon), noe vi skal vise senere. Dersom instrumentene ikke er perfekt korrelert med tanke på kursutvikling, vil porteføljens risiko understige den vektede summen av investeringsrisikoen. Dette kalles diversifisering, og er grunnleggende innen porteføljeteorien. Volatiliteten beregnes som kvadratroten av variansen. I formelen nedenfor ser vi at man ved beregningen av variansen også tar hensyn til korrelasjonskoeffisienten ρ. Så lenge denne ikke får verdien 1, oppnår vi diversifisering, dvs. når alt annet er likt kan vi redusere vår risiko ved å legge til ytterligere et aktivum i porteføljen. Variansen i porteføljeavkastningen beregnes som:
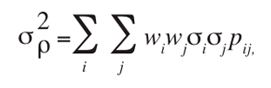
Porteføljens volatilitet målt som standardavvik blir da:
Korrelasjon
Korrelasjon er et mål på hvordan to aktiva samvarierer, i dette tilfellet hvordan prisene på to aktivum beveger seg i forhold til hverandre.
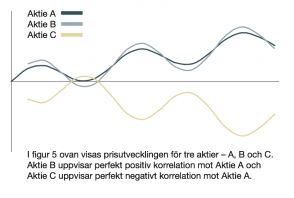
Det er trolig at en A- og B-aksje i samme selskap vil ha stor samvariasjon. I dette tilfellet vil korrelasjonskoeffisienten nærme seg 1, og diversifiseringseffektene blir små. Det er med andre ord ingen god risikospredning å kjøpe A- og B-aksjer i samme selskap. To aksjer i samme bransje vil trolig samvariere i høy grad en stor del av tiden. Kursutviklingen vil imidlertid ikke vise nøyaktig samme mønster, da den til dels blir styrt av utviklingen i bransjen generelt, men også av utviklingen i det spesifikke selskapet. Ser man isteden på korrelasjonen mellom forskjellige typer aktiva, som obligasjoner, eiendom og råvarer, ser man ofte liten samvariasjon og en korrelasjonskoeffisientsom nærmer seg null. Aktivaklasser som har en negativ korrelasjon beveger seg i motsatt retning, og når prisen på det ene aktivumet stiger, faller prisen på det andre aktivumet. Korrelasjonskoeffisienten er i dette tilfellet negativ. Aktiva med negativ korrelasjon kan være vanskelig å finne, men er verdifulle i en portefølje fordi de kan redusere porteføljens risiko betydelig.
Diversifisering (spredning av risiko)
En diversifisert portefølje oppnås ved å inkludere flere forskjellige aktivaklasser med lav innbyrdes korrelasjon. Historisk sett har råvarer, aksjer og obligasjoner hatt en tendens til å ha en relativt lav korrelasjon. Litt kuriosa: Den såkalte investeringsklokken skal ha dukket opp for første gang 1937 i avisen Evening Standard, og er en teori om aktivaprisenes koblinger til konjunkturen. Teorien sier at du skal kjøpe obligasjoner i en konjunkturnedgang når renten går ned, og aksjer i bunnen av konjunkturen da de skal ligge foran den faktiske utviklingen økonomien og får en oppgang tidlig i konjunkturen. Når økonomien er på bedringens vei og etterspørselen øker, vil råvareprisene utvikle seg best og på toppen av en konjunktur, når rentene er høye, skal man investere i korte renter eller ha pengene på konto. Investeringsklokken kan være en bra tommelfingerregel, selv om det i dag ikke er helt lett å avgjøre hvor vi befinner oss i konjunktursyklusen. Dessuten har vi i senere tid opplevd finansielle kriser som gjør at tidligere sammenhenger ikke lengre gjelder.
Risikoen i fond
Det er betydelig vanligere at fond har definert et mål for avkastning enn et mål for risiko. Dette betyr i så fall at risikoen blir en konsekvens av forvalterens strategier for å oppnå avkastningsmålet. Et regionalt aksjefond som for eksempel et Norge-fond er sjelden spesielt godt diversifisert fra et risikominimeringsperspektiv. Aksjer på det norske markedet har en tendens til å samvariere (ha høy korrelasjon). Mange hedgefond har derimot som mål at den risikojusterte avkastningen skal overstige et bestemt nivå. Risikojustert avkastning innebærer å maksimere avkastningen med hensyn til den risiko som tas. Dersom fondet tar en høyere risiko, skal det være for at avkastningen kan bli høyere.
Sharpe ratio
I fondsverdenen er Sharpe ratio (eventuelt Sharpe-forholdstallet, eller Sharpe-indeks) et vanlig mål på risikojustert avkastning. Navnet kommer fra Nobelpristakeren Willam F. Sharpe og defineres som:
Der R er aktivumets avkastning, Rf er den risikofrie renten, og E(R-Rf) er den forventede meravkastningen sammenlignet med den risikofrie renten. σ er meravkastningens volatilitet. Her antas det at det er en konstant risikofri rente over hele perioden. Sharpe-indeksen har til hensikt å vise hvor godt et aktivum kompenserer for risikoen. Jo høyere forholdstall desto bedre.
Aktiv risiko
Et annet mål på risiko som ofte blir brukt er den aktive risikoen, også kalt Tracking Error. Den aktive risikoen beskriver volatiliteten mellom porteføljens avkastning i forhold til referanseindeksen. Den aktive risikoen beregnes som:
Der Xi er forskjellen mellom fondets avkastning og indeksens avkastning for periode i og N er antallet observasjoner.
Information ratio
Information Ratio (IR) er et risikojustert mål som forteller hvor mye meravkastning en forvalter har bidratt til målt mot den aktive risikoen forvalter tok (Tracking Error). Positiv Information Ratio (alt over null) tilsier at forvalter har gitt meravkastning, og desto større verdi desto mer har forvalter bidratt med meravkastning. Negativ, eller tall i nærheten av null, tilsier at forvalter enten ikke har gitt meningsfull risikojustert meravkastning eller mistet avkastning i forhold til referanseindeksen.
Information ratio utregnes ved å ta meravkastning og dele på tracking error.
Moderne porteføljeteori (MPT)
MPT er basert på teorien om porteføljediversifisering. Teorien går ut på at man ved å optimere valget av aktiva og deres vekter skal kunne maksimere avkastningen gitt en viss risiko, eller minimere risikoen gitt en viss avkastning. Et viktig konsept innen MPT er den effektive fronten (effektive porteføljer). Hvis man legger inn alle mulige valgbare aktiva i et diagram med risikoen på x-akselen og avkastningen på y-akselen, vil man siden kunne koble sammen den venstre kanten av området med en linje, den effektive fronten. Den effektive fronten viser forskjellige muligheter for å maksimere avkastning i forhold til risiko. Befinner du deg innenfor den effektive fronten, kan du alltid finne et aktivum som enten har lavere risiko med samme avkastning, eller samme risiko men høyere forventet avkastning. Det er med andre ord ingen grunn til å velge aktiva som ikke ligger på en effektive fronten.
Den effektive fronten og MPT er matematiske modeller som bygger på relativt begrensede antagelser, noe som medfører at teorien kan skille seg fra virkeligheten, og at diversifisering virker forskjellig under forskjellige forhold. I teorien er samvariasjonen (korrelasjonen) mellom forskjellige aktiva konstant. I virkeligheten har det ofte vist seg at samvariasjonen mellom prisene på forskjellige aktiva øker når hele markedet faller sammen, eller hele land står overfor en konkurs. Dette innebærer at diversifiseringen ofte virker dårligst når man trenger den mest. En fremgangsrik porteføljeforvalter har mange faktorer å ta hensyn til, blant annet avkastning, risiko og innbyrdes korrelasjon mellom forskjellige aktiva. Dessuten bør man ha en strategi for hvordan man skal handle hvis disse parametrene endres. Ved et stort sammenbrudd vil volatiliteten stige, og risikofylte aktiva blir enda mer risikofylte og vil helt dominere risikoen i porteføljen. Det som tidligere kunne oppleves som godt diversifisert kanskje absolutt ikke er det.
Diversifiserbar og ikke diversifiserbar risiko
Spesifikk risiko er risikoen i et enkelt aktivum, og denne risikoen kan reduseres ved å inkludere flere aktiva i porteføljen. For at den spesifikke risikoen skal elimineres, kreves imidlertid at porteføljen er tilstrekkelig stor, slik at hvert enkelt aktivum bare i liten grad påvirker porteføljen som helhet. Den risiko man sitter igjen med i porteføljen, er den risikoen som ikke kan diversifiseres bort. Hvis vi setter diversifiseringen på spissen, og inkluderer alle tenkelige aktiva i porteføljen, får vi en portefølje der den eneste risikoen er markedsrisikoen.
Alfa og Beta
De greske bokstavene α (alfa) og β (beta) dukker ofte opp når man snakker om porteføljeforvaltning. Et aktivums β er et mål på hvor følsom aktivumet er for markedsrisikoen. Dersom β er > 1 betyr det at aktivumet svinger mer enn markedet. Kjøper man et indeksfond som reflekterer et bestemt marked pleier det å kalles en β-eksponering. Søker man β-eksponering på det norske aksjemarkedet, kan man således kjøpe et indeksfond som følger en av de brede norske indeksene, for eksempel OBX Index. Et aktivt forvaltet fond forsøker isteden å skape α ved å avvike fra indeks. Dersom et fond følger en indeks, kan den per definisjon ikke skape α.
(Kilde: Granit Fonder)
January 23, 2013 Leave a comment
Livet kan bare forstås baklengs,
men det må leves forlengs.Søren Kierkegaard
January 8, 2013 Leave a comment
Serien ‘Hvem tror du at du er’ på NRK1, hvor kjente norske personligheter graver tilbake i sine slektsrøtter, er ikke bare god underholdning, men belyser også på en god måte hvilken fantastisk velstandsutvikling vi har hatt i Norge. Med gripende personlige historier i en hverdagslig ramme får vi en innsiktsfull leksjon i sentrale sosialøkonomiske sammenhenger. I disse dager hvor nybegrepet ‘naving’ kanskje er blitt et symptom på mange av velstandsutfordringene vi står overfor, gir dette viktige perspektiver for bedre å forstå vår samtid.
Som serien viser så skal vi bare få generasjoner bakover i tid, før vi ser at det å dekke de grunnleggende behov var det som dominerte hverdagen til folk. Det å sørge for levelige boforhold og mat på bordet for familien var utfordringer store nok når man hadde en tallrik barneflokk. Mange av historiene forteller også om menn som velger minste motstands vei og stikker fra familien. Den gjenværende mor blir alene med å bære byrdene, og familien dras ytterligere ned i fattigdommens harde grep.
Den økonomiske veksten vi har hatt i Norge de siste hundre år har selvsagt mange forklaringer. For å forstå disse er begrepet ‘verdiskaping’ sentralt. Det representerer både en verdistørrelse på hvor mye som skapes og en verdistørrelse på hvor mye som kan etterspørres. I litt forenklede termer: hvis en persons dagsverk selges til 100, så er dette også den verdien som den samme personen kan benytte til å dekke sine behov. Dekkes de grunnleggende behov for 80, så er det 20 igjen for annen anvendelse. For både individ og nasjon er det viktig at så mye som mulig av talent og kapasitet forløses til verdiskaping. Likeså er det viktig at de metoder og prosesser som benyttes sammen med arbeid og kapital er gjenstand for en løpende utvikling, slik at man hele tiden evner å øke verdiskapingen fra samme mengde arbeid og kapital.
Hva er så forklaringen på den sterke veksten i verdiskapingen i Norge?
I forhold til å forløse talent og kapasitet blir den “protestantisk arbeidsmoral” ofte trukket frem som en viktig faktor. Forskning indikerer at sysselsettingen er høyere i land hvor protestantisk kristendom er den mest utbredte religionen. Dette forklares med at protestantismens vektlegging av hardt og flittig arbeid blant sine tilhengere, har utviklet en nasjonal kultur hvor hardt arbeid verdsettes høyere enn hva som er tilfelle i land som domineres av andre religioner. Sentralt er også den utviklingen i demokratisering og likestilling vi har vært gjennom de siste hundre år. Gjennom sosial utjevning og demokratisering har vi innrettet samfunnet slik at all talent og kapasitet kan utnyttes, ikke bare den som tilhører bestemte lag i samfunnet. Likeledes har kvinners likestilling og deres inntog i arbeidslivet gitt en sterk økning i tilgjengelig mengde talent og kapasitet for inntektsbringende verdiskaping.
Utvikling av metode og prosess er nært knyttet til de resonnementer som ble gitt i forhold til flittighet. På samme måte som vi har hatt en kulturell oppfordring til å jobbe hardt, så har det vært tilsvarende oppfordring i forhold til å gjøre ting på en bedre måte (forbedring) og på en alternativ måte (innovasjon). Begge deler gir store bidrag til verdiskapingen.
De ekstra verdier vi er tilført gjennom utvinning av de olje- og gassreserver som ble funnet på den norske kontinentalsokkelen på slutten av 60-tallet, har hatt en særskilt betydning for den økonomiske utvikling i Norge. Til tross for den store verdien som denne ekstragevinsten vil representere enda i mange år, så er det vår base av arbeid, kapital og produktivitet som utgjør vårt langsiktige grunnlag for verdiskaping.
Utviklingen i Norge de siste hundre år viser at man best bekjemper fattigdom, både nasjonalt og internasjonalt, ved å legge til rette for størst mulig verdiskaping. Jo mer man skaper av verdier til fordeling, jo lettere er det å fordele.
Fordeling av verdier som skapes er derimot i større grad et politisk spørsmål, og det er det demokratiske grunnlaget i landet som bestemmer hvordan verdier vil bli fordelt. Befolkningen i land med tilnærmet samme demokratiske nivå, kan variere ganske mye i sitt syn på hva som er en riktig fordeling. For eksempel har det demokratiske flertall i USA et ganske forskjellig syn på hvordan verdier skal fordeles, enn hva det det tilsvarende flertall i Norge har. Det er selvfølgelig ikke slik at det amerikanske folk, alternativt det norske folk, på noen måte er noe bedre eller dårligere enn andre.
Utfordringer oppstår imidlertid hvis mengden verdier som skapes i et land avhenger av hvordan det demokratiske flertall innretter fordelingen av de verdier som skapes. Derom strides imidlertid fortsatt både leg og lærd.
Fotballfaglig hjelpeverktøy for trenere av CSK J17
Med skråblikk på samfunn og økonomi.
Med skråblikk på samfunn og økonomi.
The Markets News and Analysis Blog
Fri Arena 